离散优化的求解方法

参考书目：《Optimization in Operations Research》 Chapter 12

12.1 全枚举法

12.2 离散优化模型的松弛模型及其应用

12.2.1 约束条件的松弛

定义12.4 如果($p$)的每一个可行解都是($\overline{p}$)的可行解，并且两个模型具有同样的目标函数，则我们称模型($\overline{p}$)是模型($p$)的约束条件松弛(constraint relaxation)。

12.2.2 线性规划松弛

定义12.6 连续松弛linear programming relaxation(如果给定模型是整数线性规划，则也称线性规划松弛)是一种约束条件的松弛：保留所有其他约束，但将任何离散变量都看成连续变量。

12.2.3 修改目标函数的松弛模型

定义12.8 对于优化问题($P$)和优化问题($P$)，如果(i)每一个($P$)的可行解在($R$)中也都可行，并且(ii)($P$)中的每个可行解在($R$)中的目标值与其在($P$)中的目标相比都相等或更好，那么优化问题($R$)是优化问题($P$)的松弛。

12.2.4 用松弛模型证明不可行性

松弛的一个作用就是用来证明原问题的不可行性。

1.对于一个给定的整数规划问题，线性松弛是去掉模型中的整数约束，拉格朗日松弛是放松模型中的部分线性约束，保留整数约束和其他的线性约束。

Theorem 1：如果一个模型的松弛模型是不可行的，那么它的原模型也是不可行的。（因为原模型中的每个解在松弛模型中均可行）（一个不可行的松弛确实可以得出原模型无解，但一个可行的松弛却并不意味着原模型是可行的。）

12.2.5 松弛给出最有目标值界限

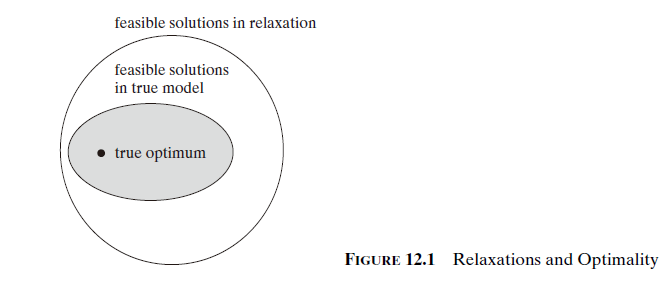
Theorem 2 ：对于求最大值的模型，其任何松弛模型的最优值都是原模型的最优值上界；类似的对于求最小值的模型，其任何松弛模型的最优值都为原模型提供了最优值下界。

12.2.6 利用松弛模型得到最优解

有时松弛模型不止能给出对应离散模型最优值的界限，甚至能给出最优解。

Theorem 3 ：如果一个约束条件松弛模型的最优解在原模型中也可行，那么这个解就是原模型的最优解。（需保证松弛问题中的目标值与原问题的目标值相同，也就是没有对目标函数进行变动）

12.2.7 松弛模型的取整解

Theorem 12.13 许多松弛模型得到的最优解都可以通过简单的取整，成为完整模型很好的可行解。

Theorem 12.14 一个最大化离散优化问题任一（整数）可行解的目标函数值，给出了整数最优值的下界。一个最小化离散优化问题任一（整数）可行解的目标函数值，给出了整数最优值的上界。

12.2.8 更强的线性规划松弛模型

Theorem 12.15 同样是正确的整数线性规划建模，却可能带来完全不同的线性规划松弛最优解。

12.2.9 选择大M常量

Theorem 12.16 当一个离散模型中需要足够大的大M时，最强的松弛模型中，常数取最小有效值。

12.3 分支定界搜索(branch and bound)

12.3.1 部分解

Theorem 12.17 一个部分解具有一些固定不变的决策变量，和其他的自由（free)或不确定的决策变量。我们使用#来表示部分解中那些自由变量。

12.3.2 部分解的完全形式

Theorem 12.18 一个给定模型的部分解的完全形式，是符合部分解中全部固定分量要求的可能的完整解。

12.3.3 树搜索

Theorem 12.19 分支定界搜索从初始的或称根本的（root）部分解$x=(#,…,#)$出发，其中所有分量都是自由变量。

Theorem 12.20 当其要么找到一个最优的完全形式，要么证明出不包含任何比已知的最佳可行解对应目标函数值更好的可行解，我们称分支定界搜索终止。

Theorem 12.21 在一个0-1离散优化模型的分支定界搜索中，当一个部分解不能被终止时，它需要被分支（branched），这通过固定之前一个自由二元变量产生两个子部分解来实现。这些部分解中的每个解都满足分出来的两个节点的约束，而不同的是，一部分符合选择固定的自由变量为1的情况，一部分符合选择固定的自由变量为0的情况。

Theorem 12.22 分支定界搜索的停止条件是，对于树中的每个部分解，要么已经被分支郭，要么已经被终止。

12.3.5 候选问题

定义12.26 在一个优化模型中，与任一部分解相关的候选问题（candidate problem），是部分解中某些变量固定时对应的受限模型。

Theorem 12.27 任一部分解可行的完全形式，就是其相应的候选问题的可行解。因此，最优可行完全解的目标值，就是候选问题的最优目标值。

12.3.6 通过松弛模型终止部分解

Theorem 12.28 如果一个候选问题的松弛模型被证明不可行，那么其相关的部分解就可以被终止了，因为它没有可行的完全形式。

Theorem 12.29 如果候选问题的任何松弛模型有不优于当前最佳解值得最优目标值，则与其对应的部分解可以被终止，因为其没有可行的完全形式可以使最优解更优。

Theorem 12.30 如果一个最优解对一个候选问题的任何约束条件的松弛模型都是可行的，那么这个最优的可行解就是相应部分解的最优完全形式。在检查是否还有新的最佳解被发现之后，我们便可以对这个部分解进行终止。

12.3.7 基于线性规划的分支定界法

算法12A：基于线性规划的分支定界法（对于0-1整数规划）

步骤0：求初始解。让唯一的活跃部分解所有离散变量均自由，并初始化解索引$t\leftarrow$0。若模型的任一可行解巳知，同样选择最优的作为最佳解$\hat x$，并记录其目标值$\hat v$。否则，若是求最大化的模型，令$\hat v \leftarrow - \infty$；若是求最小化的模型，令$\hat v \leftarrow +\infty$。

步骤1：停止。如果活跃的部分解存在，选择一个作为$x^{(t)}$，并且执行步骤2.否则，停止。如果已经存在最佳解$\hat x$，则它是最优的，如果不存在最佳解，则模型是不可行的。

步骤2：松弛。尝试求解一个与$x^{(t)}$对应的候选问题的线性规划松弛模型。

步骤3：通过不可行终止。若线性规划松弛模型被证明不可行，部分解$x^{(t)}$没有任何行的完全形式。终止$x^{(t)}$，增加$t \leftarrow t+1$，然后回到步骤1。

步骤4：通过定界终止。当模型为最大化模型且线性规划松弛模型最优值$\widetilde{v}$满足$\widetilde{v} \leq \hat v$或模型为最小化模型且有$\widetilde{v} \geq \hat v$，部分解$x^{(t)}$最优可行的完全形式不能使最佳解更优。终止$x^{(t)}$，增加$t\leftarrow t+1$，然后回到步骤1。

步骤5：通过求解终止。当线性规划松驰模型的最优解$\widetilde x^{(t)}$满足模型中所有的二元约束，这个最优解就是部分解$x^{(t)}$的最优可行的完全形式。保存这个最佳解为最新的最佳解:

$$\hat x \leftarrow \widetilde x^{(t)}$$ $$\hat v \leftarrow \widetilde v$$

之后，终止$x^{(t)}$，增加$t\leftarrow t+1$，然后回到步骤1。

步骤6：分支。选择线性规划松弛最优解中某些为分数的自由二元约束分量$x_p$，并且通过分支$x^{(t)}$的方法产生两个新的活跃解。一个是将$x_p$分量固定为0，其余分量均与$x^{(t)}$保持相同；另一个是将$x_p$分量固定为1，其余分量与$x^{(t)}$保持相同。之后，增加$t\leftarrow t+1$，然后回到步骤1。

12.3.8 基于线性规划的分支定界法的分支规则

Theorem 12.31 基于线性规划的分支定界算法总是通过对候选问题的松弛模型中非整数的分量施加一个整数约束来完成分支。

Theorem 12.32 当松弛最优解中有不止一个整数变量取值为分数的时候，基于线性规划的分支定界算法通常通过固定一个最接近整数值的分量来进行分支。

12.4 分支定界法的改良

12.4.2 最佳解整数化

Theorem 12.33 如果方便取整，分支定界搜索中每个不能被终止的部分解的松弛最有解，通常在进行分支前取整，形成完整模型的可行解。如果这个可行解比其他已知解更好，那么它就提供了一个新的最佳解。

12.5 分支切割法(branch and cut)

12.5.1 有效不等式

定义12.41 如果一个线性不等式对于一个离散优化模型的所有（整数）可行解都成立，那么这个线性不等式就是这个给定离散优化模型的有效不等式。

Theorem 12.42 为了加强一个松弛模型的有效性，一个有效不等式必须切割（使不可行）一些在现在松弛模型中可行，但是在完全整数规划模型中并不可行的解。

12.5.2 分支切割搜索

分支切割算法在枚举过程进行下去的时候，动态结合了有效不等式和分支定界搜索。

定义12.43 分支切割算法通过在分支一个部分解之前， 尝试用新的有效不等式来加强松弛模型的有效性，进而加强了分支定界算法所代表的的基础分支定界策略。新增的约束应该切割掉最新得出的松弛模型的最优解。