双重差分法，英文名Differences-in-Differences，别名“倍差法”，小名“差中差”。作为政策效应评估方法中的一大利器，双重差分法受到越来越多人的青睐，概括起来有如下几个方面的原因：（1）可以很大程度上避免内生性问题的困扰：政策相对于微观经济主体而言一般是外生的，因而不存在逆向因果问题。此外，使用固定效应估计一定程度上也缓解了遗漏变量偏误问题。（2）传统方法下评估政策效应，主要是通过设置一个政策发生与否的虚拟变量然后进行回归，相较而言，双重差分法的模型设置更加科学，能更加准确地估计出政策效应。（3）双重差分法的原理和模型设置很简单，容易理解和运用，并不像空间计量等方法一样让人望而生畏。（4）尽管双重差分法估计的本质就是面板数据固定效应估计，但是DID听上去或多或少也要比OLS、FE之流更加“时尚高端”，因而DID的使用一定程度上可以满足“虚荣心”。
作者：经管联盟链接：https://zhuanlan.zhihu.com/p/48952513来源：知乎著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

参考链接(作者：经管联盟)

Ashenfelter 和 Card（1985）首次引入 DID 模型来解决此问题，继而该模型的应用开始得到越来越多的重视。

DID仅适用于面板数据，基准DID模型设置如下：

$$Y_it = \alpha_0+\alpha_1du+\alpha_2dt+\alpha_3du \cdot dt+\epsilon_{it} \tag{1}$$

其中，$du$为分组虚拟变量，若个体$i$受政策实施的影响，则个体i属于处理组，对应的$du$取值为1，若个体$i$不受政策实施的影响，则个体$i$属于对照组，对应的$du$取值为0。$dt$为政策实施虚拟变量，政策实施之前$dt$取值为0，政策实施之后$dt$取值为1。$du·dt$为分组虚拟变量与政策实施虚拟变量的交互项，其系数$\alpha_3$就反映了政策实施的净效应。

从DID的模型设置来看，要想使用DID必须满足以下两个关键条件：一是必须存在一个具有试点性质的政策冲击，这样才能找到处理组和对照组，那种一次性全铺开的政策并不适用于DID分析；二是必须具有一个相应的至少两年（政策实施前后各一年）的面板数据集。

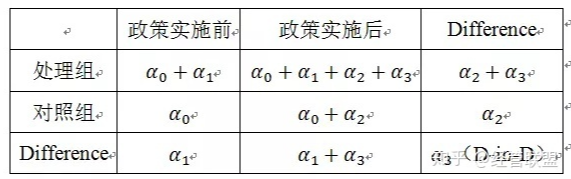
双重差分法的基本思想就是通过对政策实施前后对照组和处理组之间差异的比较构造出反映政策效果的双重差分统计量，将该思想与上表的内容转化为简单的模型（1），这个时候只需要关注模型（1）中交互项的系数，就得到了想要的DID下的政策净效应。

更进一步地，DID的思想与上表的内容可以通过下图来体现：

图中红色虚线表示的是假设政策并未实施时处理组的发展趋势。事实上，该图也反映出了DID最为重要和关键的前提条件：共同趋势（Common Trends），也就是说，处理组和对照组在政策实施之前必须具有相同的发展趋势。DID的使用不需要什么政策随机以及分组随机，只要求CT假设，因此用DID做论文时必须对该假设进行验证，至于具体怎么验证，后面再说。

很多时候，大家在看使用DID的文献时，会发现别人的基准模型和模型（1）并不完全一致，别人的模型如下：

$$Y_{i t}=\alpha_{0}+\alpha_{1} d u \cdot d t+\lambda_{i}+v_{t}+\varepsilon_{i t} \tag{2}$$

别人的模型里只有交互项$du·dt$，而缺失了$du$和$dt$，是哪里出问题了么？并没有，模型（1）和（2）本质还是一样的，且模型（2）在多年面板数据集里更为常见。

模型（2）中，$\lambda_i$为个体固定效应，更为精确地反映了个体特征，替代了原来粗糙的分组变量$du$；

$v_t$为时间固定效应，更为精确地反映了时间特征，替代了原来粗糙的政策实施变量$dt$。因而，$du$和$dt$并未真正从模型中消失，只是换了个马甲。模型（2）事实上就是一个双向固定效应模型，这也是为什么DID方法一定程度上可以减轻遗漏变量偏误的原因（主要是消除那些不可观测的非时变因素，为了使估计结果尽可能准确，模型中还是要加入控制变量）。

在介绍完DID的基本思想和模型设定后，现在要开始强调同等重要的内容，那就是稳健性检验——必须证实所有效应确实是由政策实施所导致的。很多人对这一点并不重视，认为DID很简单，随便跑几个回归就可以写出一篇大作了。关于DID的稳健性检验，主要表现在两个方面：

（1）共同趋势的检验。这个假设是比较难验证的，看文献时会发现别人经常没有做该检验，比如，很多人做DID时只有政策实施前后各一年的数据，这样的的话根本无法验证政策实施前的趋势问题。不过，如果是多年的面板数据，可以通过画图来检验CT假设，之前推荐的那篇AER文章就画了大量的图形对此进行了说明。

（2）即便处理组和对照组在政策实施之前的趋势相同，仍要担心是否同时发生了其他可能影响趋势变化的政策，也就是说，政策干预时点之后处理组和对照组趋势的变化，可能并不真正是由该政策导致的，而是同时期其他的政策导致的。这一问题可以概括为处理变量对产出变量作用机制的排他性，对此，可以进行如下的检验：

A. 安慰剂检验，即通过虚构处理组进行回归，具体可以：a）选取政策实施之前的年份进行处理，比如原来的政策发生在2008年，研究区间为2007-2009年，这时可以将研究区间前移至2005-2007年，并假定政策实施年份为2006年，然后进行回归；b）选取已知的并不受政策实施影响的群组作为处理组进行回归。如果不同虚构方式下的DID估计量的回归结果依然显著，说明原来的估计结果很有可能出现了偏误。

B. 可以利用不同的对照组进行回归，看研究结论是否依然一致。

C. 可以选取一个完全不受政策干预影响的因素作为被解释变量进行回归，如果DID估计量的回归结果依然显著，说明原来的估计结果很有可能出现了偏误。等等。

例子：参考链接

我们假设浙江省政府仅在杭州、嘉兴与湖州（简称杭嘉湖）三个地区的各乡镇实行了一项经济改革试验，而现在的任务是对改革的绩效进行评价。假设横向比较的结果是，杭嘉湖地区在改革后的绩效高于没有进行改革的浙江非杭嘉湖地区的绩效，那么我们能否认为这就是改革取得成功的证据呢？答案是不确定的，其理由是：杭嘉湖地区与非杭嘉湖地区若在改革之前就存在绩效差异，则改革后两个地区的绩效差异很可能继承了改革之前的绩效差异。因此，仅仅对改革后的绩效进行横向比较，无法准确评估杭嘉湖地区改革的净效应。

现在进行纵向比较。如果杭嘉湖地区改革前后的绩效出现非常明显的变化，那么我们能否认为这就是改革取得成功的证据呢？若在杭嘉湖地区改革前后，浙江非杭嘉湖地区同期也发生了相同幅度的变化，则答案很可能是否定的，理由是：既然在非杭嘉湖地区没有实行改革，那么这些地区发生的同等变化就应该与改革无关。我们可以认为，杭嘉湖地区与非杭嘉湖地区发生的同等变化是源于全国宏观经济形势与浙江整体经济形势的变化。

若在杭嘉湖地区改革前后，浙江非杭嘉湖地区同期发生了较小的变化，则对上述问题的回答就是肯定的 。当然，在进行纵向比较时，我们必须施加共同趋势假定，即：如果杭嘉湖地区未实行改革试验，那么也会发生与非杭嘉湖地区相同的较小变化。可以认为， 浙江非杭嘉湖地区发生的较小变化是源于全国宏观经济形势与浙江整体经济形势的变化， 而杭嘉湖地区之所以有较大变化，是因为还存在额外的改革绩效。

实行改革的杭嘉湖地区就是所谓的处理组，而实行的改革就是实施的处理。相应的， 未实行改革的非杭嘉湖地区就是对照组。在对处理组实施处理的前后，对照组亦会发生或大或小的变化。如果在评估改革绩效即评估处理效应时，没有将处理组与对照组的变化进行同期对照，那么我们所发现的处理效应很可能存在偏差。在本文的例子中，杭嘉湖地区改革前后的绩效变化具有三个来源：全国宏观经济形势变化、浙江整体经济形势变化、改革绩效。如果没有与非杭嘉湖地区的变化进行同期对照，那么我们评估的改革绩效就混杂了全国宏观经济形势与浙江整体经济形势变化的影响，因此很可能存在较大偏差。

鉴于非杭嘉湖地区作为对照组，其绩效变化可以代表全国宏观经济形势与浙江整体经济形势变化的影响，一个简单有效的纠偏方法就是：通过对杭嘉湖地区的绩效变化与非杭嘉湖地区的绩效变化进行比较，将全国宏观经济形势与浙江整体经济形势变化的影响从杭嘉湖地区的绩效变化中一并剔除，进而获得净的处理效应，而这正是双重差分模型的基本逻辑。

建立 DID 模型首先需设立两个虚拟变量：

$$D_{1}=\left\{\begin{array}{l}{1 \qquad \text{浙江杭嘉湖地区}} \\ {0\qquad \text{浙江非杭嘉湖地区}}\end{array}\right. \qquad D_{2}=\left\{\begin{array}{l}{1 \qquad \text{改革后}} \\ {0\qquad \text{改革前}}\end{array}\right.$$

然后建立模型：

$$Score_{i}=\alpha_{0}+\alpha_{1} D_{1 i}+\alpha_{2} D_{2 i}+\alpha_{3} D_{1 i} \cdot D_{2 i}+\varepsilon_{i}$$

在这里，i 代表各乡镇，Score 代表绩效评价指标；参数a0代表改革前所有乡镇共同的初始绩效均值；a1 代表杭嘉湖地区与非杭嘉湖地区在改革前的初始绩效差异；a2 代表杭嘉湖地区与非杭嘉湖地区在改革前后共同发生的绩效变化，即共同趋势，具体是指全国宏观经济形势与浙江整体经济形势变化的影响；a3 代表在控制了初始绩效差异与共同趋势之后，杭嘉湖地区所具有的额外绩效变化，此即改革绩效。

在所有参数中，a2 与 a3 是最为关键的。为了进一步理解这两个参数的含义，接下来我们对虚拟变量赋值，有：

1） 对于浙江非杭嘉湖地区（D1=0）：

改革后（D2=1）的期望绩效为：a0 +a2 ；

改革前（D2=0）的期望绩效为：a0 。

因此，浙江非杭嘉湖地区改革前后的绩效差异为：（a0 +a2）-a0 =a2。a2 就是共同的趋势，即全国宏观经济形势变化影响与浙江整体经济形势变化影响之和。

2） 对于浙江杭嘉湖地区（D1=1）：

改革后（D2=1）的期望绩效为：a0 +a1 +a2 + a3 ；

改革前（D2=0）的期望绩效为：a0 +a1 。

因此，杭嘉湖地区改革前后的绩效差异为： a0 +a1 +a2 + a3）-（a0 +a1）=a2 + a3 。杭嘉湖地区的绩效变化是全国宏观经济形势变化影响、浙江整体经济形势变化影响与改革绩效这三者之和，而a2 是全国宏观经济形势变化影响与浙江整体经济形势变化影响之和。因此，a3 就是杭嘉湖地区的改革绩效。

杭嘉湖地区改革前后的绩效差异（a2 + a3）与同期非杭嘉湖地区绩效差异（a2）的差为 a3 。因此，改革绩效a3 属于差异的差异，从而这就解释了DID（Difference-In-Difference）称谓的来源。

上述虚拟变量模型能够被拓展：一方面，若杭嘉湖地区与非杭嘉湖地区在改革前的初始绩效差异可以用变量 x 来加以解释，则变量 x 可作为解释变量进入模型、进而改善模型估计的精度；另一方面，若 x 的差异还会造成共同趋势假设被违背，则需引入交互项 x·D2， 以控制趋势差异的影响。